1020. Веревка

В стену вбито n гвоздей так, что они образуют выпуклый многоугольник. На эти гвозди натянута веревка как показано на рисунке ниже:

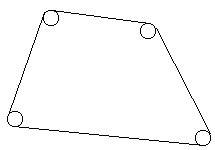
Зная координаты центров гвоздей и их радиус шляпок (он одинаковый для всех гвоздей), найти длину натянутой веревки.

Вход. Первая строка содержит количество гвоздей n (1 £ n £ 100) и радиус их шляпок r. Следующие n строк содержат координаты (x, y) центров гвоздей в порядке обхода их по часовой стрелке. Известно, что |x|, |y| £ 100 и являются вещественными числами.

Выход. Длина веревки, натянутой на гвозди. Длину выводить с двумя точками после запятой.

Пример входа

4 1

0.0 0.0

2.0 0.0

2.0 2.0

0.0 2.0

Пример выхода

14.28

РЕШЕНИЕ

геометрия

Анализ алгоритма

Длина веревки равна сумме расстояний между центрами соседних гвоздей плюс 2pr (длина обода шляпки гвоздя).

Реализация алгоритма

Объявим константу p. В массивах x и y храним координаты центров гвоздей.

#define PI acos(-1.0)

double len,r,x[100],y[100];

Читаем входные данные. Присвоим переменой len значение длины обода шляпки.

scanf("%d %lf",&n,&r);

len = 2*PI*r;

for(i=0;i<n;i++) scanf("%lf %lf",&x[i],&y[i]);

Положим (n + 1) – ую точку равной первой.

x[n] = x[0]; y[n] = y[0];

Если n > 1, то ответом будет 2pr. Иначе к значению len = 2pr следует прибавить сумму расстояний между центрами соседних гвоздей.

if (n > 1)

for(i=0;i<n;i++)

len += sqrt((x[i+1]-x[i])*(x[i+1]-x[i]) + (y[i+1]-y[i])*(y[i+1]-y[i]));

Выводим длину веревки len с двумя точками после запятой.

printf("%.2lf\n",len);